You can set the HUD to use either statistics or probabilities. Statistics show a summary of what a player has done so far. Probabilities predict what a player will do in the next hand.
To switch between statistics and probabilities, use the HUD configuration menu (the one you see in the top right-hand corner of the HUD while you play).
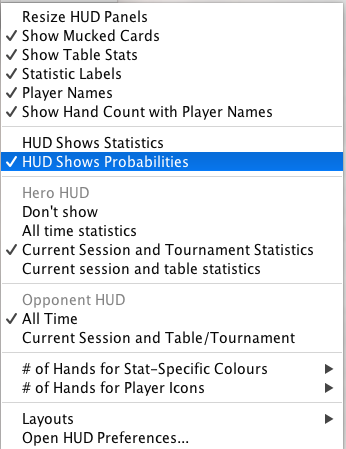
Use the HUD’s statistics mode if you want to see what a player has done so far. Use the HUD’s probabilities mode if you want to see an estimate of a player’s future action, using standard mathematical techniques.
Statistics
By default the HUD makes all calculations using statistics. It shows the actual observed behaviour of your opponents.
For example, if you’ve seen the same player twice, and both times he folded preflop, his value for VPIP will be 0%.
That’s an accurate statistic based on what you’ve seen this player do. But it is not a good prediction of what the player will do in the next hand.
That’s where using probabilities can help.
Probabilities
If you use probabilities, the HUD takes into account that just because the player has a VPIP of 0% so far, that doesn’t mean he never will put money in the pot. In fact, it would be highly inaccurate to guess the VPIP to be 0%.
But he is somewhat more likely to have a low VPIP than a high VPIP.
In the 18th century, the French mathematician Pierre-Simon Laplace found a way to estimate the probability of an event when there are only a few observations. The HUD uses Laplace’s rule of succession to estimate a player’s probable VPIP based on the statistics gathered so far.
The rule of succession is surprisingly simple, yet quite reliable in turning a statistic into a probability given a limited sample space.
In the example above, where we saw a player twice, and both times he folded preflop, the HUD will show a probability of 25% for VPIP for the next hand. After that hand the HUD will update its probability up or down, based on what the player did.
If you’d like to know more about this approach, it is a basic example of Bayesian probability.
Need more help with this?
Don’t hesitate to contact us here.